Electrostatic potential and capacitance notes are provided below and capacitance notes are present at bottom of page
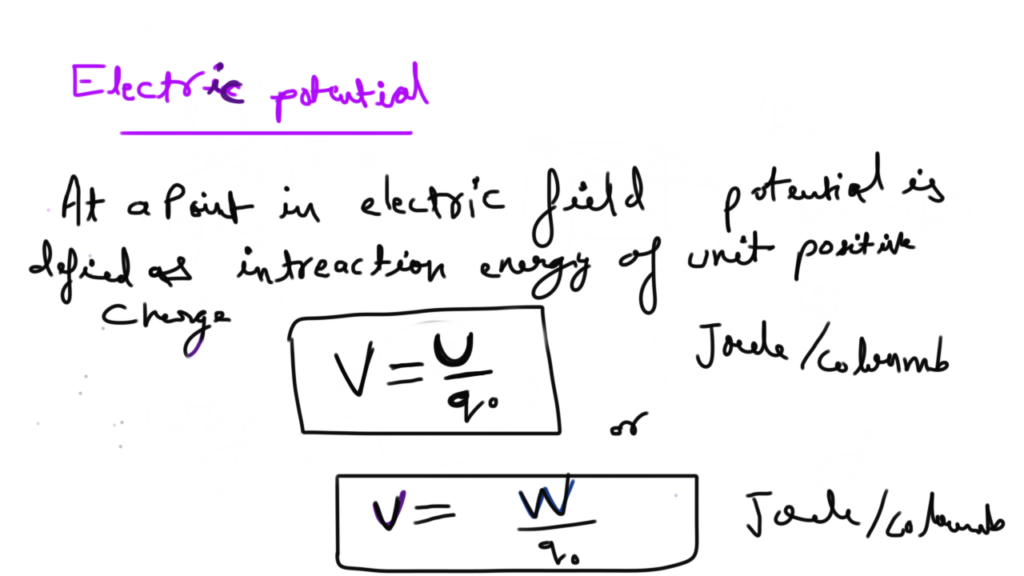
Electric potential is a scalar property of every point in the region of electric field. A point in electric field potential is the interaction energy of a unit positive charge.
let a point in electric field charge q0 has potential energy U, electric potential at that point is given by
Potential energy of a charge in an electric field is defined as the work done in bringing the charge from infinity to the given point in the electric field. Similarly we can define electric potential as work done in bringing a unit positive charge from infinity to the given point against the electric forces
Regarding potential it is worth noting that
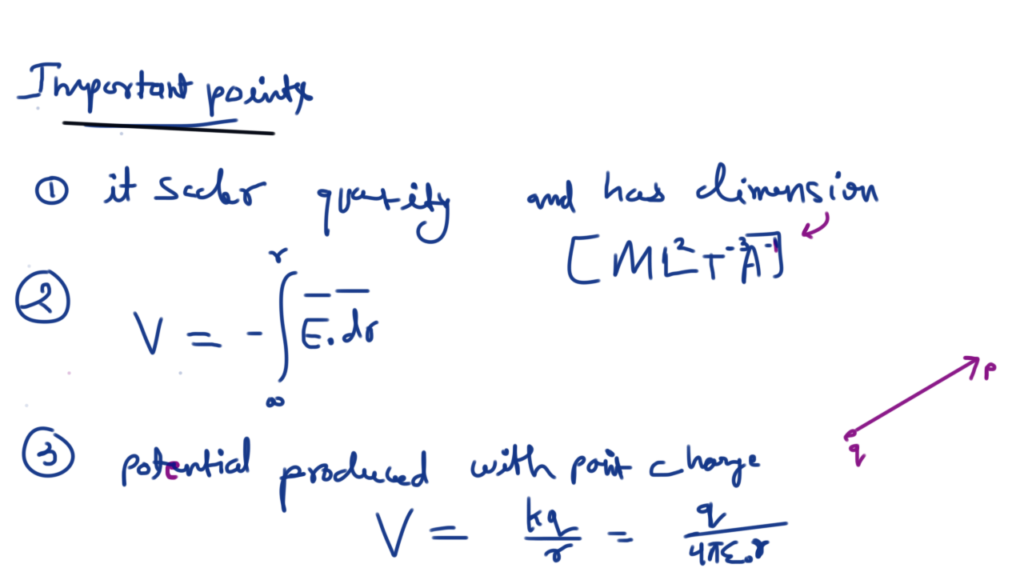
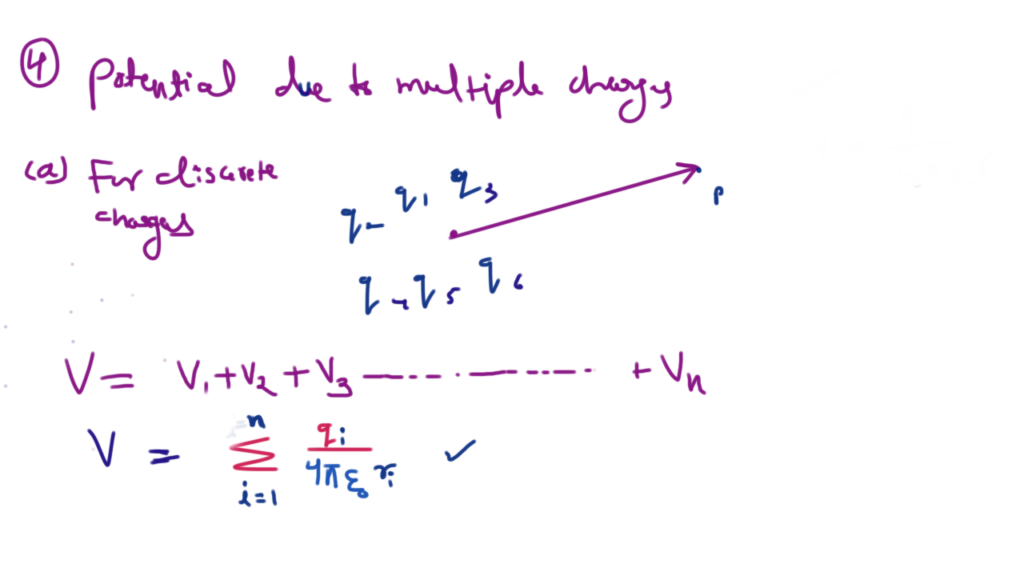

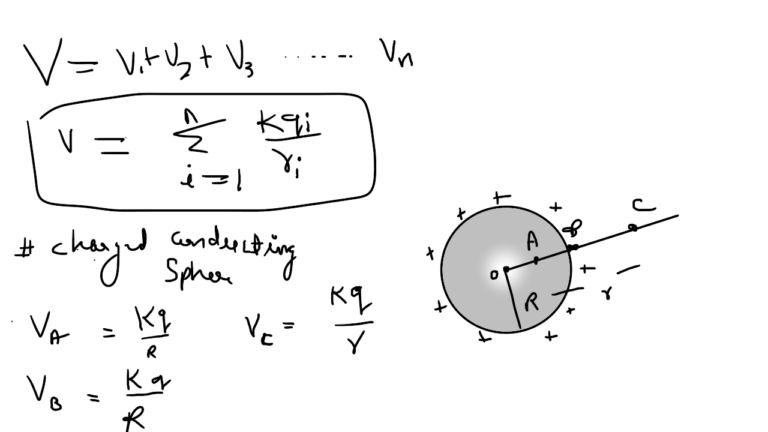
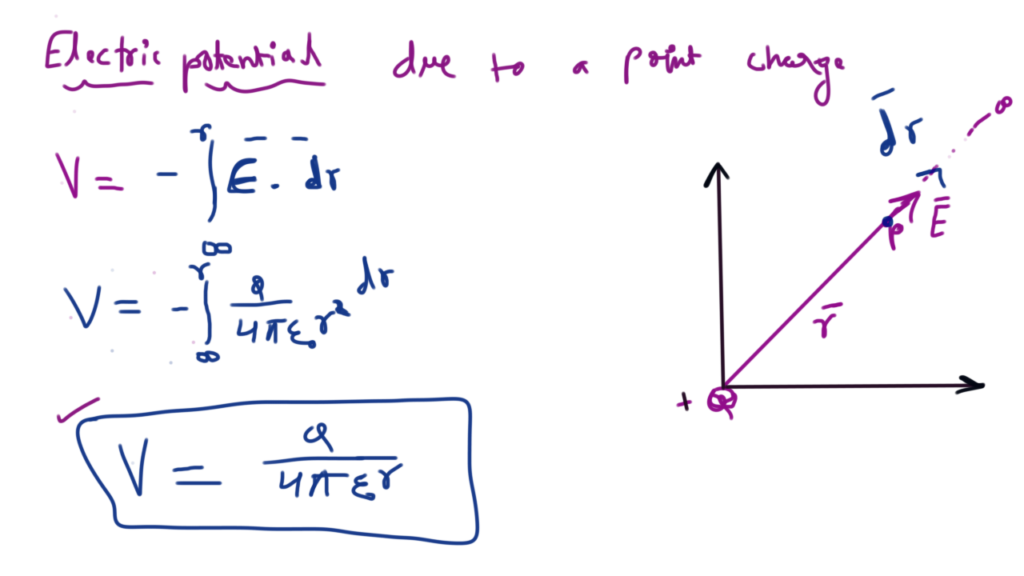
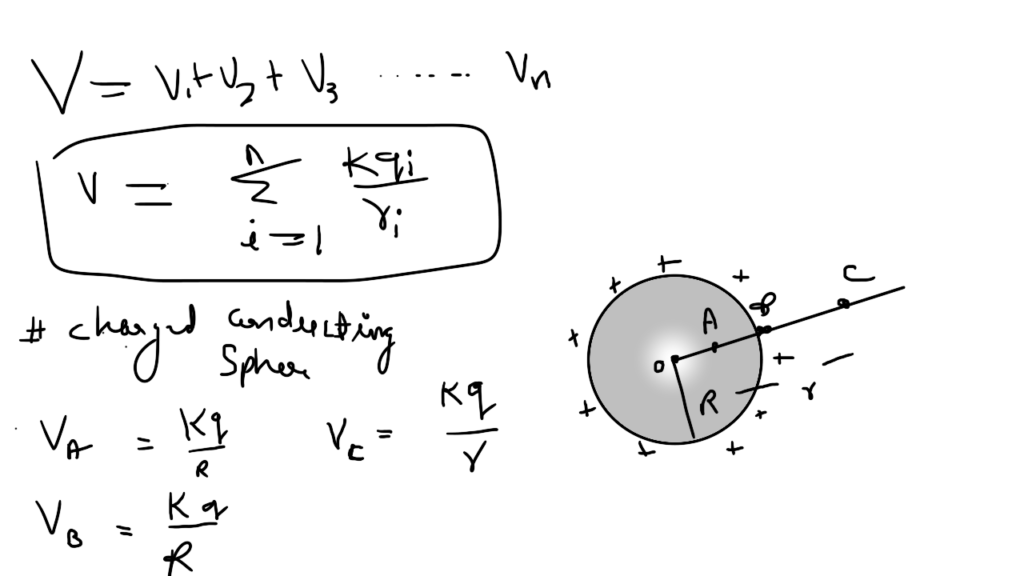
Electric Potential due to a Point Charge
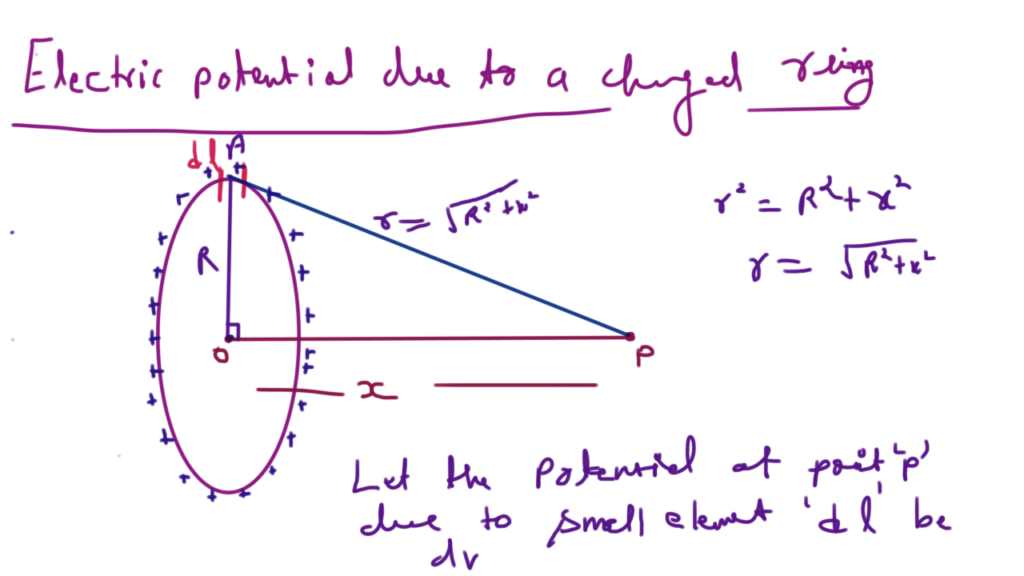
Electric Potential due to a Charged Ring
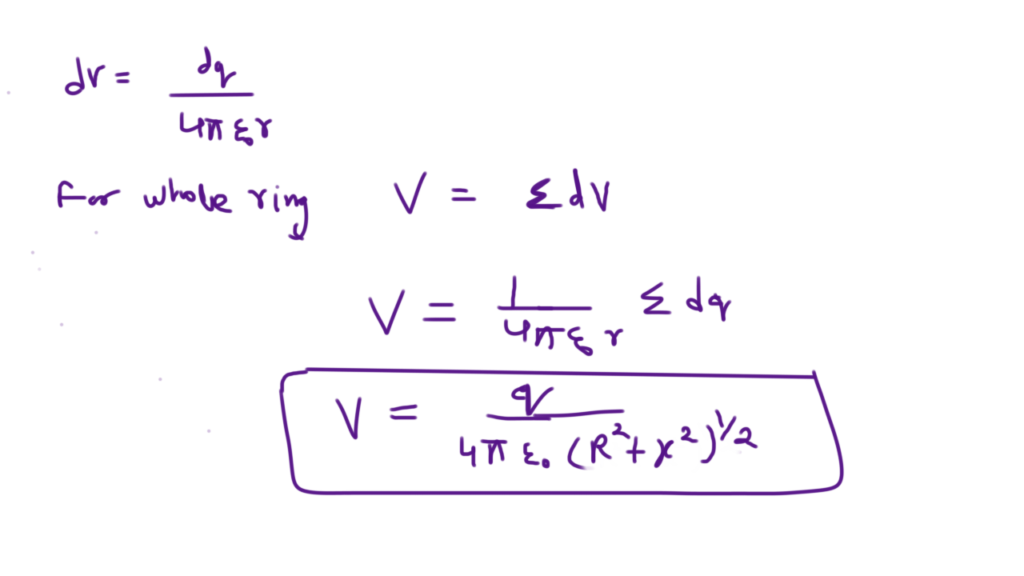
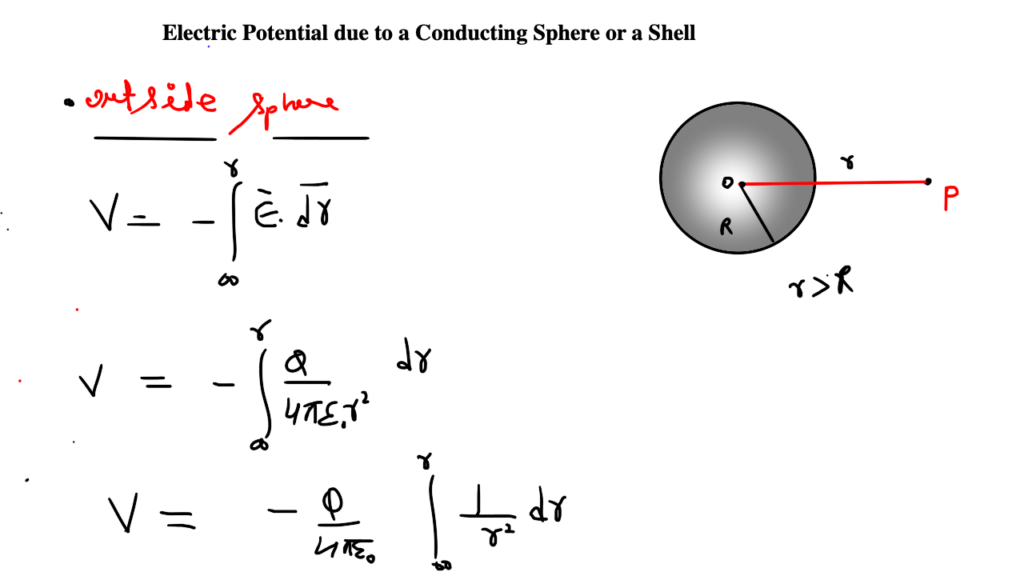
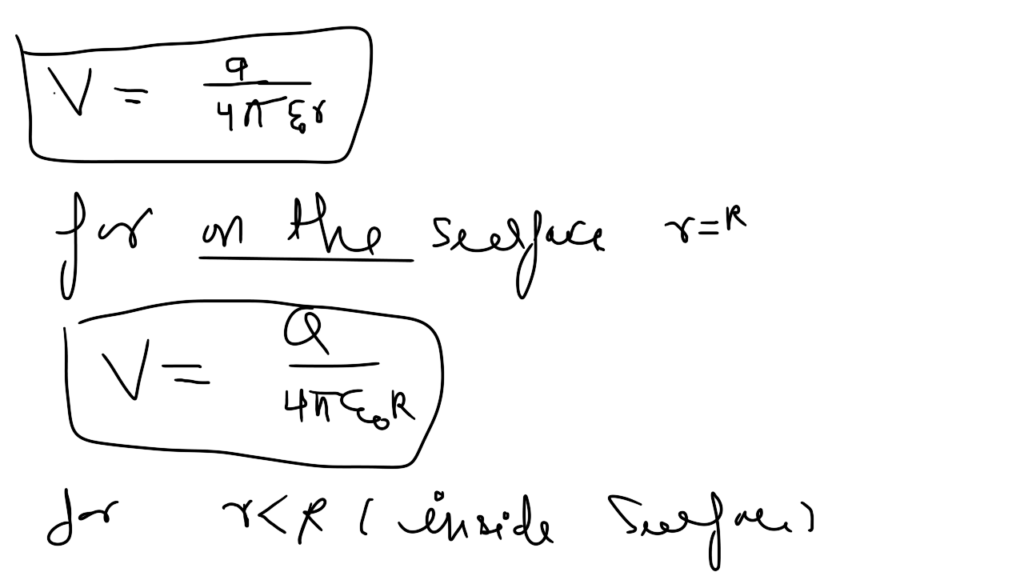

Inside the sphere
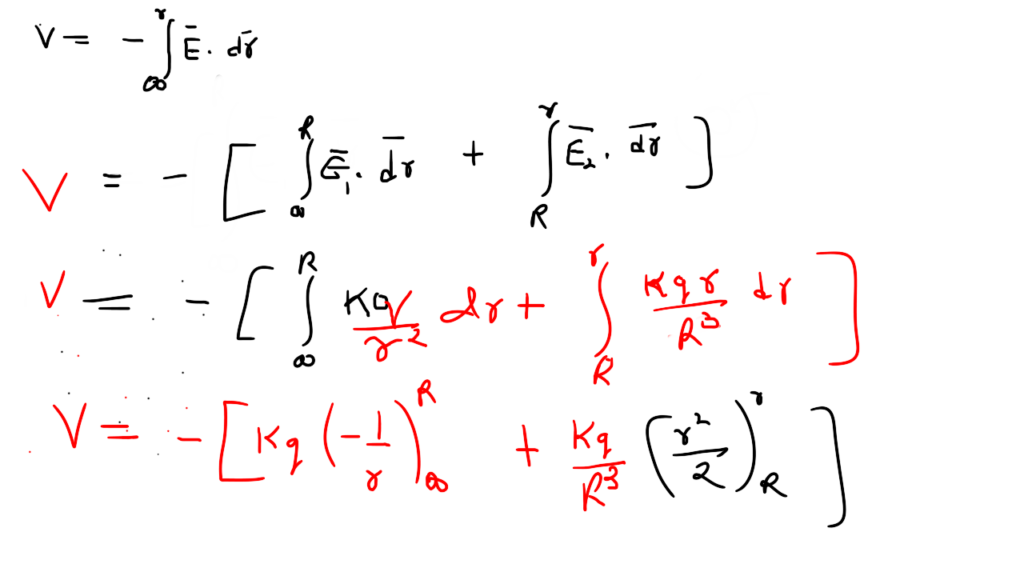
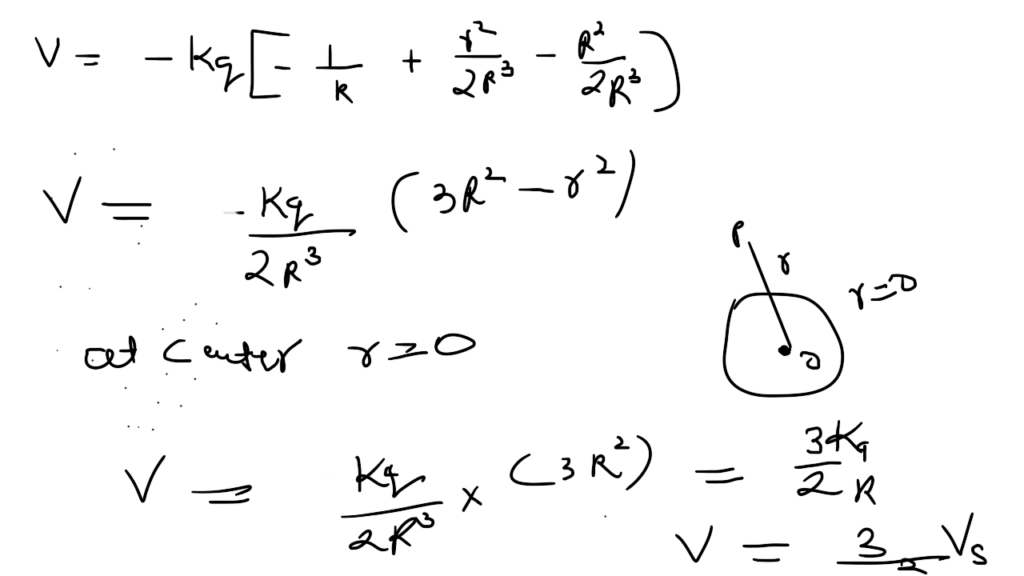


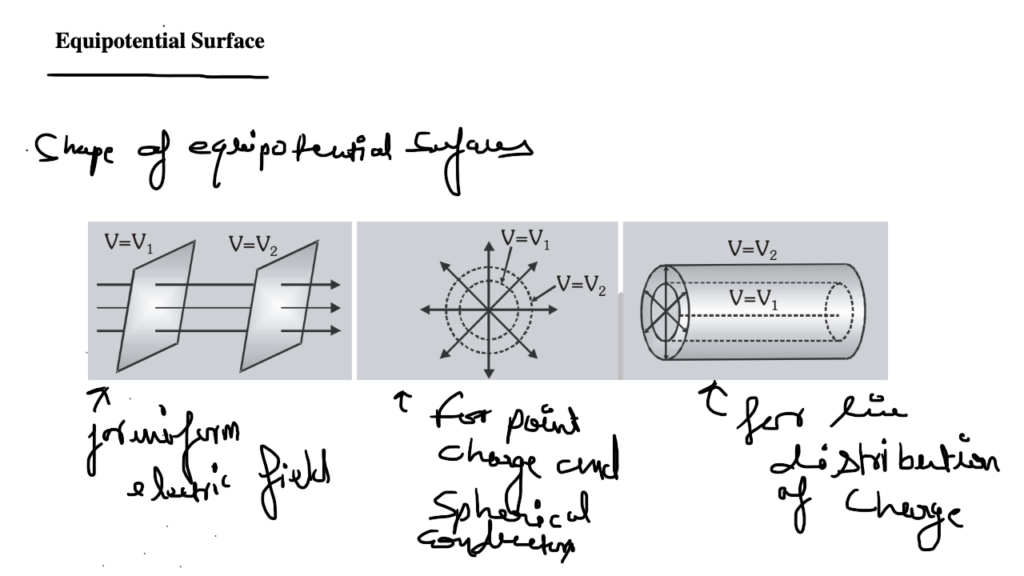
Equipotential surfaces
For a given charge distribution , the plane or surface correspoinding to the locus of all points having same potential is called ‘equipotential surface’.
l Equipotential surfaces can never cross each other (otherwise potential at a point will have two values which is absurd).
l Equipotential surfaces are always perpendicular to the direction of electric field. l If a charge is moved from one point to an other over an equipotential surface
then work done W = q(V1-V2)
If potential energy at infinity is zero, external work done in changing the configuration of a system from ‘i’ to ‘f’ is W = Uf – Ui
eV is the smallest practical unit of energy used in atomic and nuclear physics. (1 eV = 1.6 ×10–19 J)
Potential is theoretically zero at infinity; practically we consider it zero on the earth surface.
Potential on earth is assumed to be zero as it is a large conductor and its potential is more or less constant in relation to finite charge given to or taken from it.
Electric potential is the same at all points in a region in which E = 0.
Equipotential surfaces need not be physical surfaces. Any imaginary surface over which the electric field is perpendicular to it every where is called an equipotential surface.
Equipotential surfaces are closely spaced where electric field intensity is large and widely spaced where electric field intensity is small.
Electric field must be zero within an equipotential volume.
Different equipotential surfaces due to a point charge whose potentials differ by a constant amount (say 1 volt) are not equispaced. Two equipotential surfaces never intersect.
When we place a charged conductor inside a hollow conductor and connect them by a conducting wire, the charge will be completely transferred from the inner conductor to the other conductor.
Try these questions